Solid Geometry (maths) With TinkerCAD - the Volume of a Parallelepiped
2190 Views, 0 Favorites, 0 Comments
Solid Geometry (maths) With TinkerCAD - the Volume of a Parallelepiped

This lesson uses TinkerCAD and 3D printing to let students explore and verify the volume of a parallelepiped.
Learning objectives:
- maths (12-13 years): students are able to calculate the volume of a cuboid
- maths (13-14 years): students are able to derive the volume of an unknown shape by splitting the volume into known shapes
- universal skills: students are able to find different solutions to the same problem (creativity) and are able to think critically about the result
(Dutch version attached to this instructable.)
Supplies
- computer with access to Tinkercad
- 3D printer (optional)
Create an Account on TinkerCAD
Go to www.TinkerCAD.com and log in or create an account.
Let the students first get to know the basics in TinkerCAD by using the tutorials under 'Learn'.
Start With a Cuboid
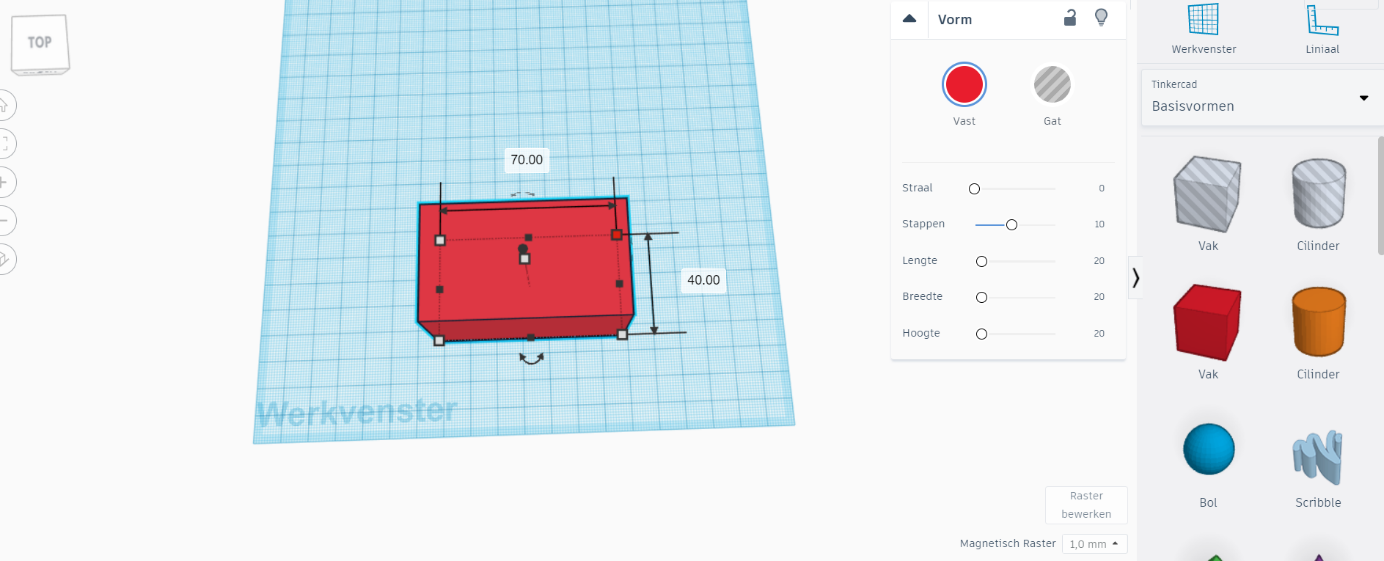
Ask your students to create a basic cuboid with predefinded dimensions (for example, 70 mm x 40 mm x 40 mm).
Let them write down the volume of this cuboid.
The Challenge: Create a Parallelepiped
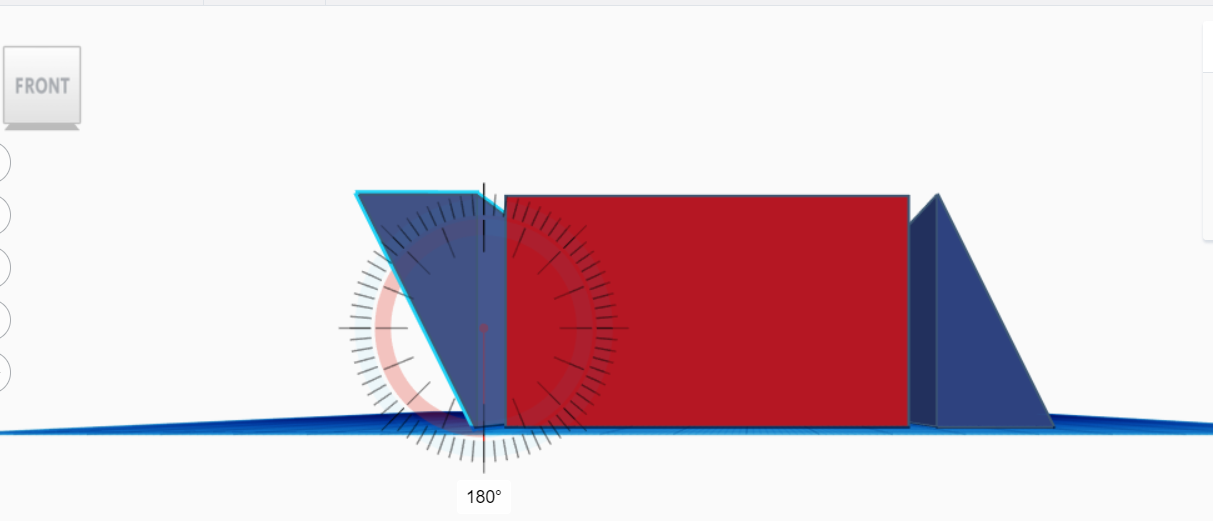
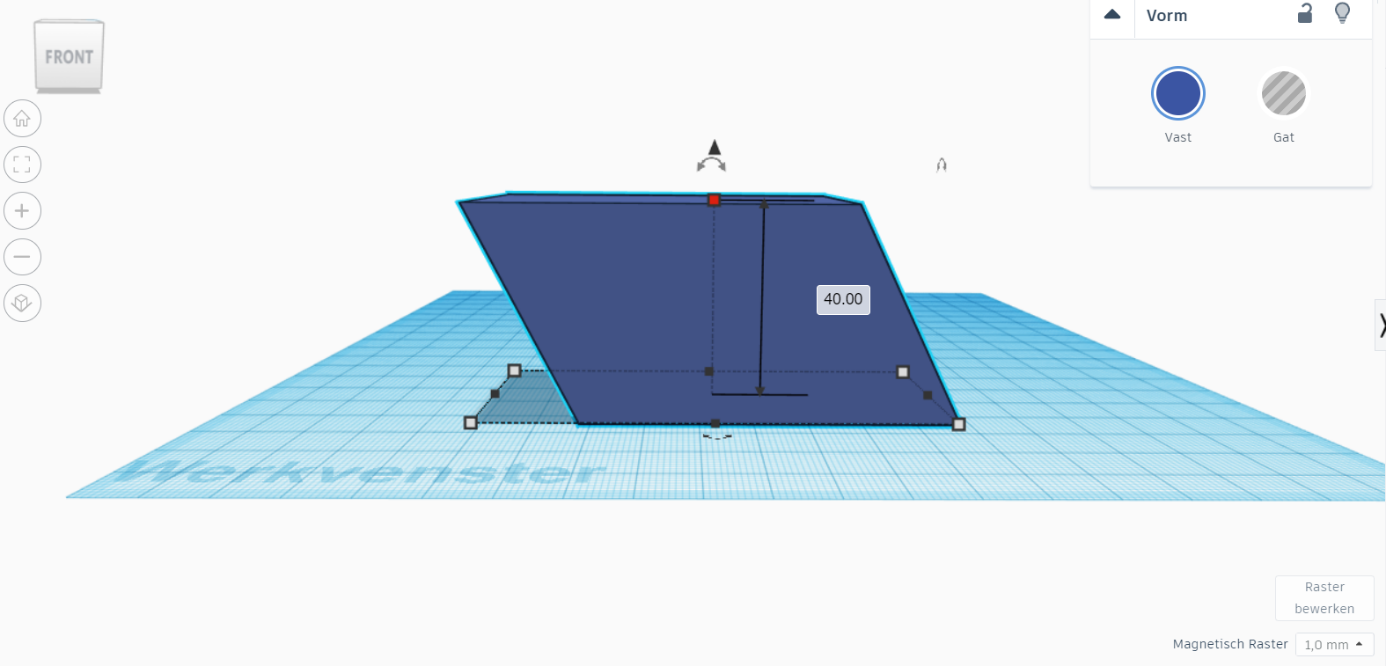
Now give your students the challenge to create a new shape that has the same volume as the cuboid, but has two parallellograms at the side instead of rectangles. They have to start from the cuboid and adapt the shape without changing the volume. They are allowed to cut (with a thin plane) and reposition pieces.
In case they need help for this challenge, one possible solution is given below: (you can also work with a thin cut plane)
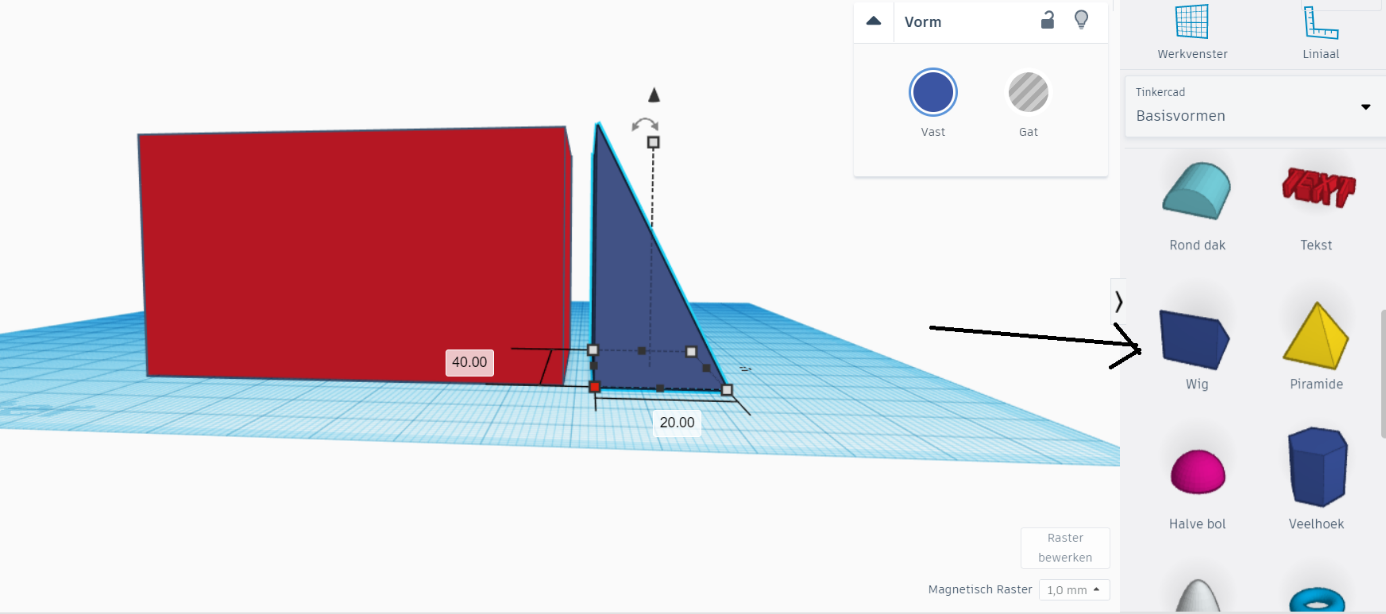
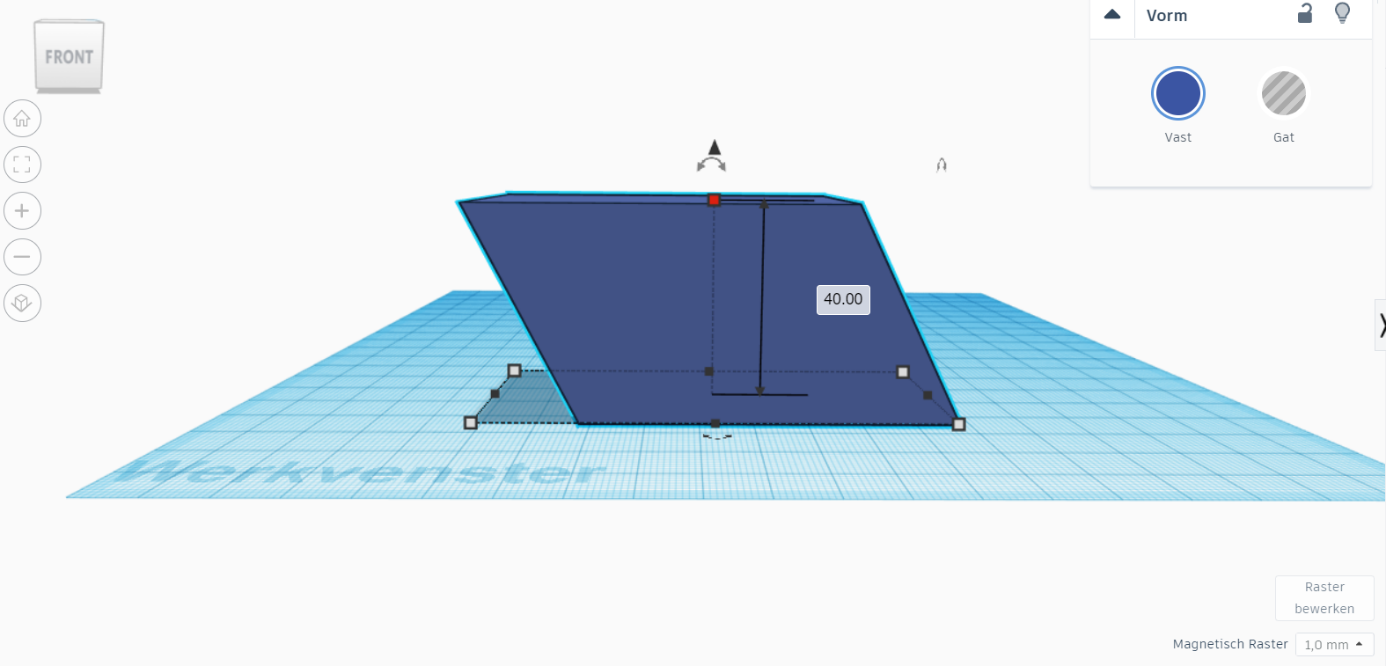
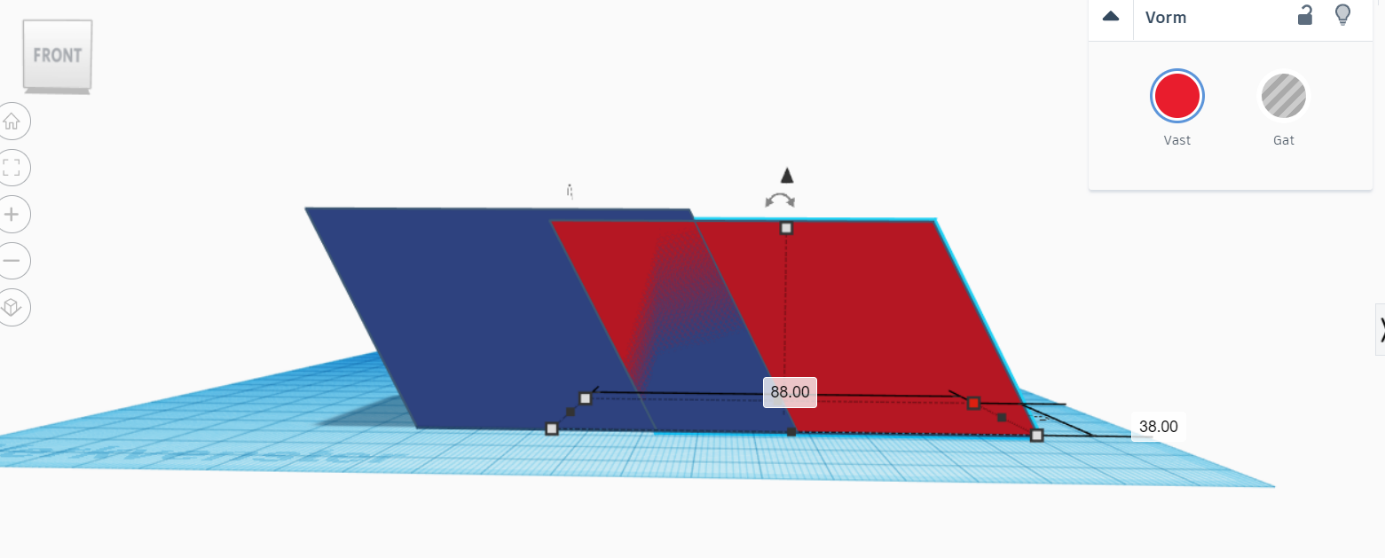
You can create a wig with one of the sides the same as the side of your cuboid. (in this case : 40 mm x 40 mm).
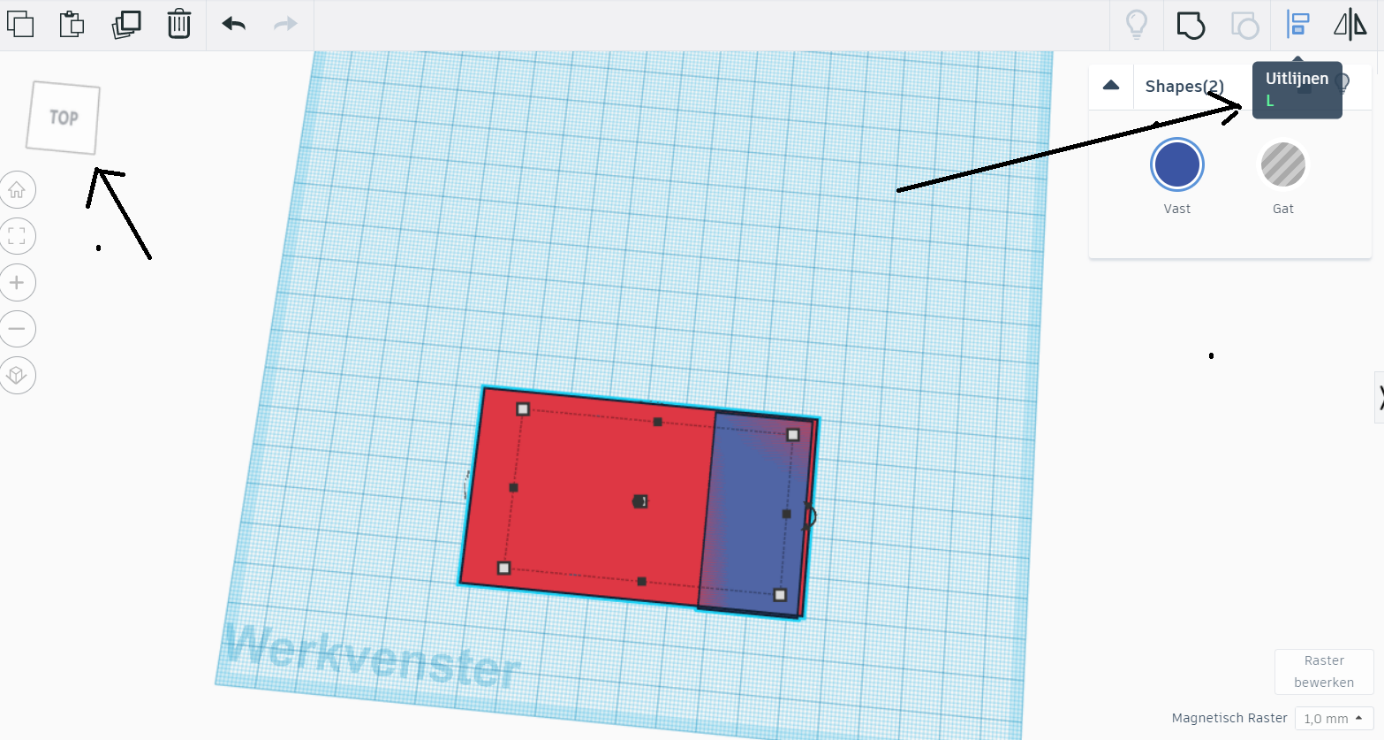
Duplicate this wig. You will once use it to cut out a wig on the cuboid and once use it to add the shape to the other side. So in total, you won't have cut away any material. (See pictures). Make sure to use the 'align' tool to precisely position the wigs.
In the end, make sure to 'group' all objects so you have one solid parallelepiped.
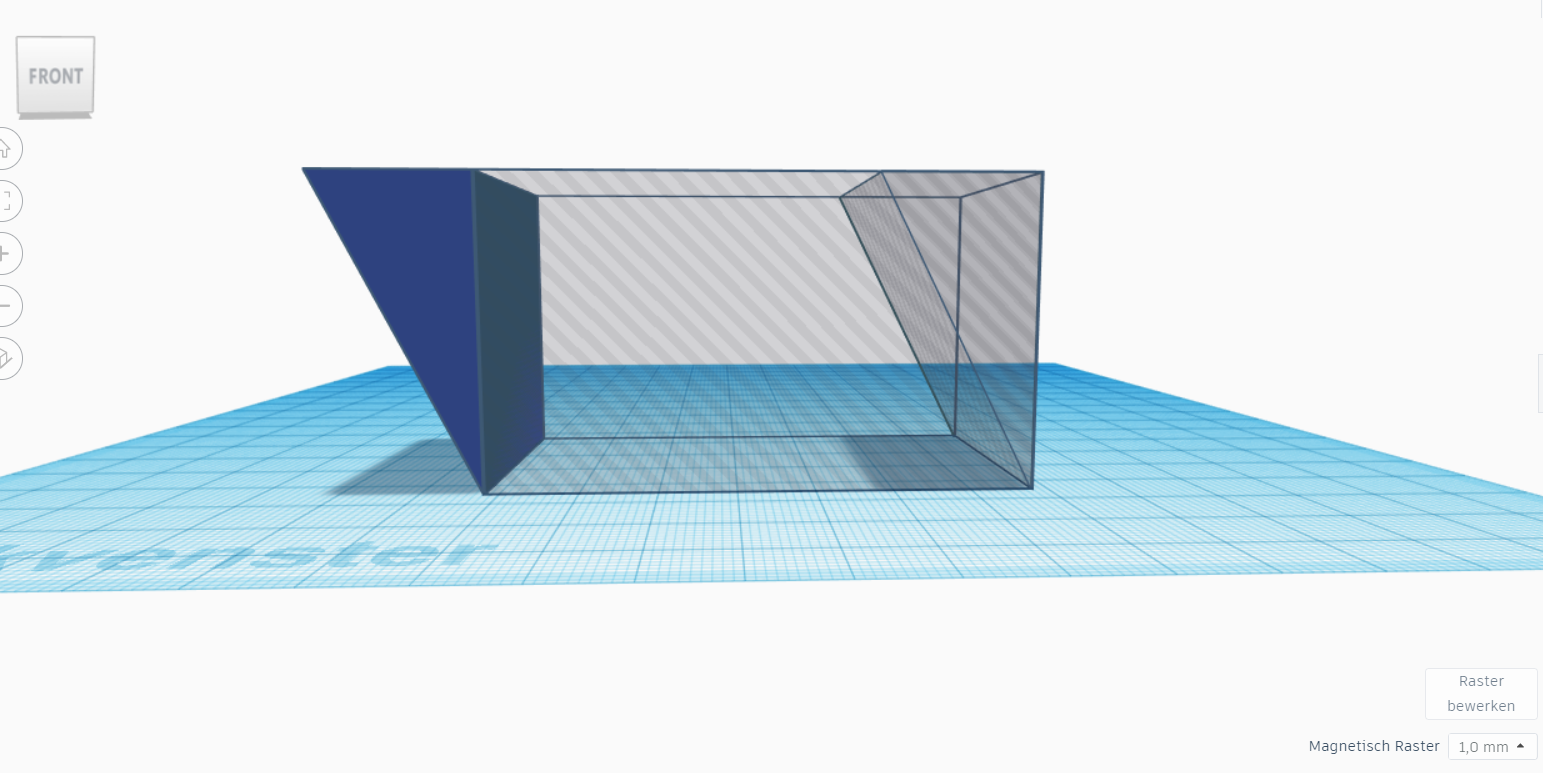
Hollow Out the Parallelepiped to Verify the Volume
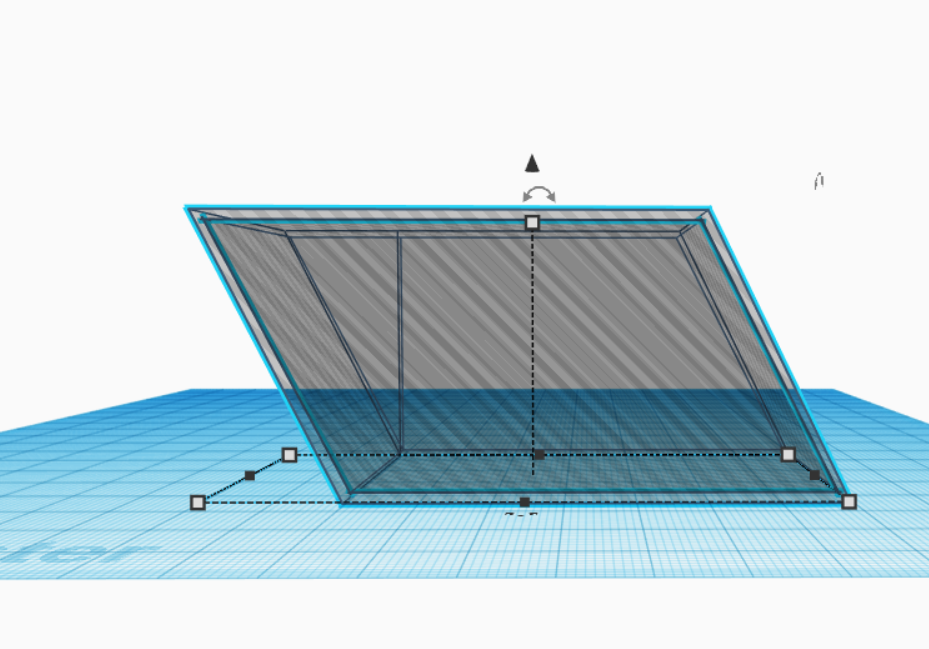
We might assume that the volume of the new created shape (parallelepiped) has the same volume as the cuboid. But how will we verify this is true? Let the students think in groups for a few minutes how they will prove this. Help them to critically think about this plan and possible hurdles.
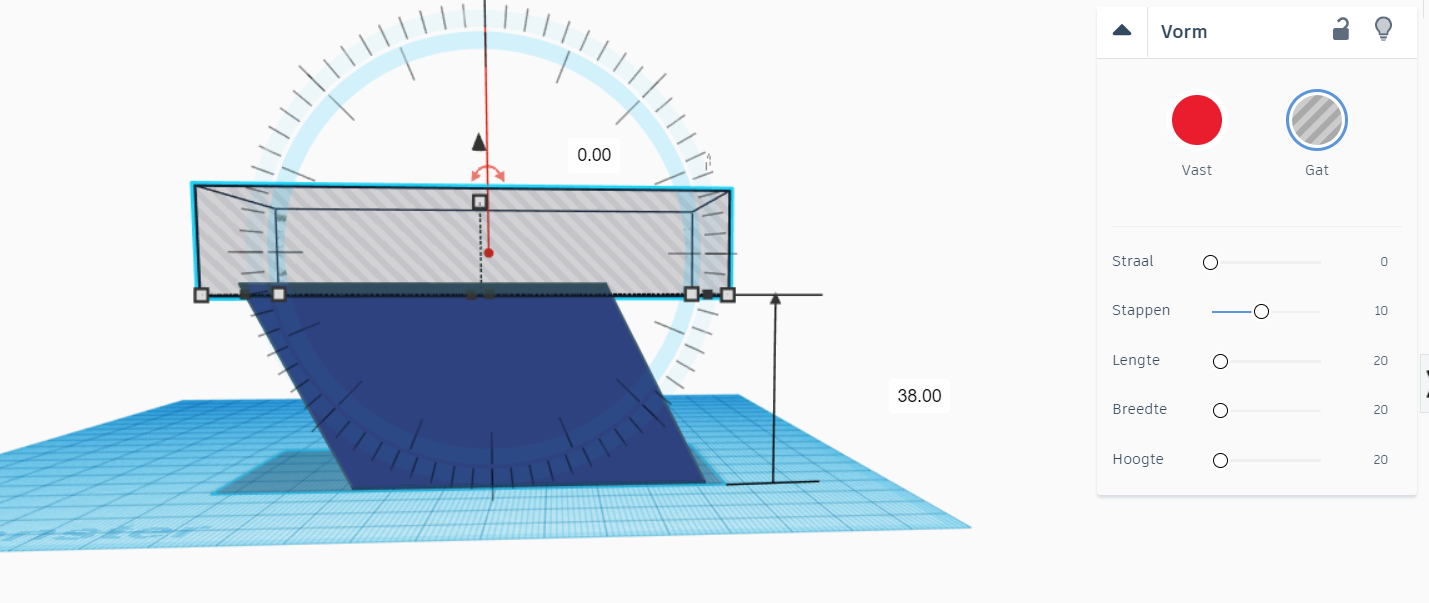
One way to do this, is to hollow the object, print it out and verify with a volume of water poured into the volume. (You can also use hard plastic and glue gun to create this object). However, doing this, you will need to take the wall thickness into account.
Duplicate the volume and make it 2 mm smaller on each side. This will serve as 'gap'. The volume you will measure with the water is this volume. You might also make it 2 mm bigger on each side (which makes it easier to calculate, otherwise, they will need to calculate the volume of the thin walls.)
Make sure to have your object open on the top! (So that there are no support structures needed and you are able to pour water in.)
Printing the Parallelepiped and Testing the Volume
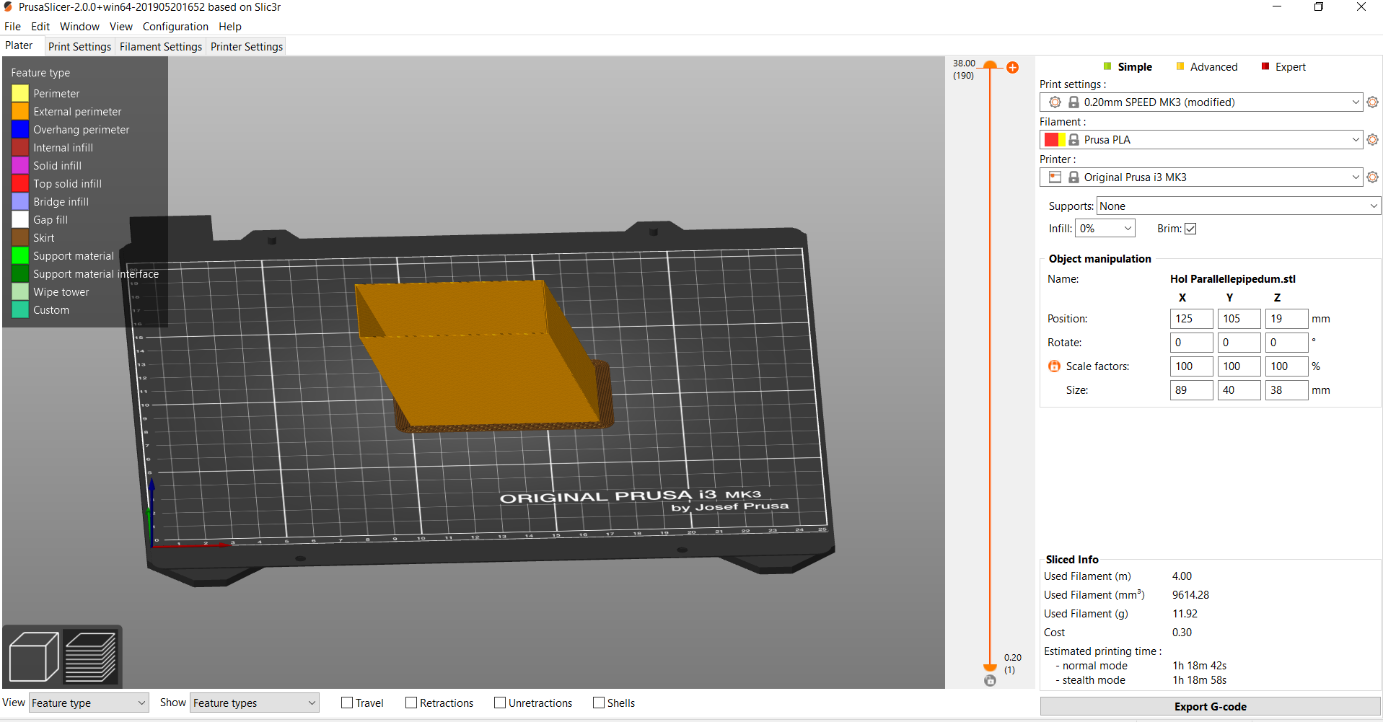


After the object is printed, you can verify the volume with water. (Pour water in it and measure the volume of water with a measuring cylinder)
Extra questions to the students:
- how much material (in grams) will the printer need to use (they have to calculate the inner and outer volume and use the mass density of the plastic)?
- how much would this cost?
You can check the answers with the calculations in the slicer program in case you're using a 3D printer to create the volume.